Roel's World Blog » Music Blog

Approx. reading time: 15 minutesJuly 1, 2016

MUSIC & GEOMETRY (The Sacred Geometry Of Music)

A note to start this article with:

Perfect geometric shapes only occur when using Equal Temperament. Sonically though the intervals of Equal Tempered instruments/music aren’t perfect (accept for the Octave). They are always a bit sharp or flat in comparison with the Harmonic Series (how sound occurs in nature) and Just Intonation.

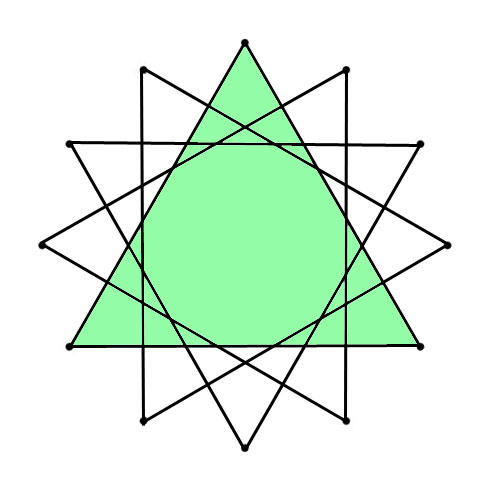
The most harmonious sounding (Just) intervals (the octave excluded) do NOT create perfect symmetrical geometric shapes!
If you “stack” one or more “type” of Just Intervals you will always end up with a spiral!

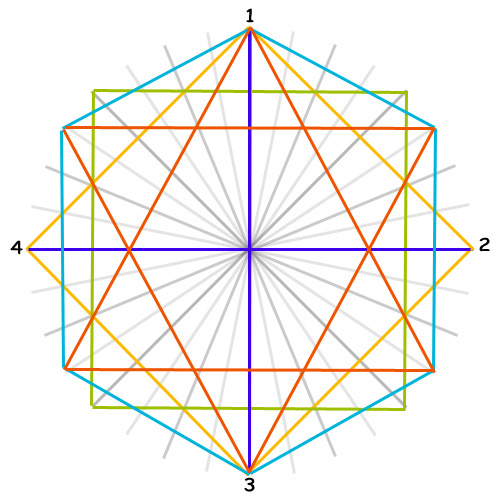
In this article all geometrically perfect shapes (trigone, square, pentagon, et cetera) thus relate to 12-Tone Equal Temperament as do any and all perfect geometrical shapes used on this blog as well as on any other blog, website and book available.

“Music theory has no self-evident foundation in modern mathematics yet the basis of musical sound can be described mathematically (in acoustics) and exhibits “a remarkable array of number properties”.
In its form, rhythm and metre, the pitches of its notes (intervals) and the tempo of its pulse music can be related to the mathematical measurement of time and frequency, offering ready analogies in geometry.”

Now, of course tones and chords are not the same “things” as for example polygons and polygrams. Units like Hertz and Degrees are not the same, they have their own function and use. But in the math behind many “things” there are formulas and ratios (relationships) that are very similar, if not identical. Would it thus be too ‘far-fetched’ to say that the same “rules” apply for many – if not all – things in the universe?

This article will “zoom-in” into geometry in particular.

Skip “INTRODUCTION (ABOUT 12-TONE CIRCLES)” AND …

INTRODUCTION (ABOUT 12-TONE CIRCLES)

In Western music theory there are 13 intervals from Tonic (unison) to Octave. These intervals are the: Unison, Minor Second, Major Second, Minor Third, Major Third, Fourth, Tritone, Fifth, Minor Sixth, Major Sixth, Minor Seventh, Major Seventh and Octave.

Note: click on the interval names for more basic info (Wikipedia). If you are interested in a more esoteric-philosophical perspective on the intervals, then read the article: “The Function of the Intervals” on Roel’s World.

When we look at these intervals and how they relate to one another in the musical tone circles, some geometric shapes appear. The most common tone circles in Western music are the “Chromatic Circle” and the “Circle of Fifths“.

The Chromatic Circle is a visualization of the Chromatic Scale and the 12-Tone Equal Temperament. Both clockwise and counterclockwise movements follow the Chromatic Scale (respectively up and down).

The Circle of Fifths is based on the stacking of (Perfect) Fifths, characteristic for the Pythagorean Temperament. If you move around the circle clockwise you go up a Fifth with every “step” you take, if you move around the circle counterclockwise you go up a Fourth with every “step” you take.

What is important to make note of though, is that the Circle of Fifths (on the right) is geometrically incorrectly drawn. In the case of the Circle of Fifths starting on C going clockwise around, the first 11 sections should be drawn a tiny bit bigger. The result of this is that the last section (F) would be relatively smaller then the other 11 sections, if you close the circle. When “Stacking” perfect Fifths the Circle isn’t closed, but creates a spiral, the C after the F slightly overshoots (approx. about the size of a Quartertone.

For perfect geometric shapes, you should always use an “Equal Temperament”. Any “Just Temperament” (based on the Harmonic Series) will not result in perfect geometric shapes.

RELATIVE MAJOR / MINOR TONALITIES

To give a “complete” picture in this introduction about tone circles you see on the right the Circle of ascending Fifths/Fourths with both Major and minor tonalities. The relationship between the Major and minor tonalities is of course the same in the Chromatic Circle.

For this article I have chosen to only us the circles with Major tonalities to have more space for drawing lines between the tones of the circle that form the geometric shapes (polygons and polygrams).

Even though the relative Major and minor are on the same side of the circle they do not automatically “replace” each other musically.

For example: the geometric relationship C Major and G♭ Major is the same as the geometric relationship between A minor and E♭ minor. The relationship between C Major and E♭ minor might look the same geometrically within the circle but is a different one! The tonic of C Major is a Tritone apart from G♭ Major, but only a minor 3rd apart from E♭ minor.

DIFFERENCES BETWEEN THE CHROMATIC CIRCLE AND THE CIRCLE OF FIFTHS:

You might have noticed that the tone circles above have different “shades of grey” for their tones. This is done for a reason. From a “philosophical” point of view you could say that – when you look at the “movement” around the circles – the Chromatic Circle represents ‘Polarity‘ and/or ‘Dualism‘ and the Circle of Fifths represents ‘Unity‘ and/or ‘Nondualism‘.

Of course the Circle of Fifths can be read counterclockwise as well, but than it would not longer be the Circle of Fifths but the Circle of Fourths instead. In other words, the Chromatic Circle is bidirectional (same interval size in both directions) and the Circle of Fifths (clockwise) unidirectional, as is the Circle of Fourths (counterclockwise).

CHROMATIC CIRCLE

When we look at the Chromatic Circle, then we can see two “poles”, C and F♯/G♭. From these “poles” we move around the circle in both directions. Now, imagine placing a “mirror” from C to F♯/G♭.

Then B is “mirrored” by C♯/D♭ (5♯/7♭ | 7♯\5♭), A♯/B♭ by D (10♯/2♭ | 2♯\10♭), A by D♯/E♭ (3♯/9♭ | 9♯\3♭), G by F (1♯/11♭ | 11♯\1♭), and G♯/E♭ by E (8♯/4♭ | 4♯\8♭). F♯/G♭ “mirrors” itself within (6♯ | 6♭) as does C (0♯ | 0♭). The numbers stay the same but the “polarity” has changed (sharp to flat, plus to minus, “male” to “female”).

The two opposites of Yin and Yang (the image on the right, turned 90 degrees to align with the tone circle) attract and complement each other and, each side has at its core an element of the other (represented by the small dots). Neither pole is superior to the other and, a correct balance between the two poles must be reached in order to achieve harmony.

To me the Yin and Yang symbol (circle) represents Octave (complete scale), the Tritone interval (geometric mean) “splits” the octave in half: black half (Yin), white half (Yang). The dots represent the two most important intervals in music, the white dot = 5th (3:2, arithmetic mean – Yang, the sun) and the black dot = 4rd (4:3, harmonic mean – Yin, the moon). Both “lead” to the opposite half, across the “border” (the Tritone), the white dot to the white half (down, 5th to the Tonic) and the black dot to the black half (up, 4th to the Octave).

CIRCLE OF FIFTHS

When going around the Circle of Fifths the build-up and decrease of the number of sharp and flats is constant. The sharps going up 0-11 while the flats go down simultaneously 11-0.And another pattern to be seen:

0 – 1 – 2 – 3 – 4 – 5 – 6 – 5 – 4 – 3 – 2 – 1 (- 0).

As you can go around this circle endlessly An natural gradualness with no beginning, no end. Ouroboros, (the tail-devouring snake). A unbroken circle, a cross-cultural symbol often representing completeness which encompasses all space and Time, “infinity” or “unity“.

GEOMETRY OF INTERVALS – ‘CONNECTING THE TONES’

There are many ways to visualize the connection between tones. One of the more “common” methods is to use geometric shapes, at least for the visual oriented persons and/or mathematical minds among us.

LINE
The simplest “shape” is a line. The “connected” tones in the Chromatic Circle and the Circle of Fifths are a “Tritone“ apart from one another: C-G♭, G-D♭, D-A♭, A-E♭, E-B♭ & B-F.The lines drawn represent Equal Tempered Tritones of 600 cents.

TRIGON (triangle)
The clockwise “connected” tones are a Major Third (400 cents) apart from one another: C-E, E-A♭ & A♭-C / G-B, B-E♭ & E♭-G / D-G♭, G♭-B♭ & B♭-D / A-D♭, D♭-F & F-A. (800 cents) apart. The triad formed by playing all 3 tones of the trigon together is called “Augmented Triad“.

SQUARE
In the Chromatic Circle the clockwise “connected” tones are a Minor Third (300 cents) apart from one another: C-E♭, E♭-G♭, G♭-A & A-C/B♭-D♭, D♭-E, E-G & G-B♭ / F-A♭, A♭-B, B-D & D-F. Counterclockwise (going up the scale) the “connected” tones are a Major Sixth (900 cents) apart.

With the Circle of Fifths you have to swap the direction to get the same interval.

A Triad formed by two legs of the square is called the “Diminished Triad“. It contains the “Devil’s Interval” (“Diabolus in Musica”) better known as “TriTone“, found in between the Tonic and (dim.) Fifth (C-G♭ & E♭-A, D-A♭ & F-B, E-B♭ & D♭-G) of the Diminished Triads. All 4 tones (square) together forms a “Diminished 7th Chord“, containing two simultaneous played TriTones a Minor Third apart.

HEXAGON
The “connected” signs form two Hexatonic or Whole Tone Scales when combined: C–D–E–G♭–A♭–B♭–C and B–D♭–E♭–F–G-A-B. The clockwise “connected” tones are a Major Second (Whole Tone, 200 cents) apart, counterclockwise (goung ip the scale) they are a Minor Seventh (1000 cents) apart.

DODECAGON
The Chromatic Circle visualize the Chromatic Scale: clockwise in Minor Second (100 cents) and counterclockwise (going up the scale) Major Seventh (1100 cents). The Circle of Fifths visualizes clockwise the Fifths (Equal Tempered 700 cents), counterclockwise the Fourths (Equal Tempered 500 cents).

DODECAGRAM
When you follow the lines of the Dodecagram across the Chromatic Circle, you find clockwise the Fifths (700 cents) and counterclockwise the Fourths (500 cents). The Circle of Fifths visualizes the Chromatic Scale: clockwise in Minor Second (Equal Tempered 100 cents) and counterclockwise (going up the scale) Major Seventh (Equal Tempered 1100 cents).

SUPERIMPOSED
With these geometric “shapes” combined, all possible tone-connections (intervals) of the 12-Tone system can be made, as is clear from the combined graph.

NOTE: As I have mentioned earlier, perfect Geometric shapes relate to the 12-Tone Equal Temperament. Just Intonated intervals are larger or smaller then the Equal Tempered ones. This means that the geometric shapes would not “close” (end where they started) or result in shapes that ain’t symmetrical.

When stacking Just Intervals a spiral appears, not a closed tone-circle such as the Chromatic Circle. So, even though Just Intonated intervals are more consonant, sound more natural (Harmonic Series), are more pleasing to the ear, the geometric shapes will be less then perfect. This by itself “proofs” (in my opinion) that a perfect geometric shape or mathematical formula does not per definition generate or represent the most perfect tone/interval/chord/scale/sound.

It is good to note though, that a spiral is considered mathematically symmetrical as well, the combination of a central dilation and a rotation whose centers are distinct is also “spiral symmetry”. Geometrically (visually) though the spiral isn’t symmetrical as the (Equal Tempered) shapes seen in the circles above that have “Reflection” (or “Mirror”) Symmetry, Rotational Symmetry and Point Symmetry.

INTERVALS SUPERIMPOSED FROM ONE TONIC (IN COLOR)
This is what all intervals related to only one tonic (in this example the tone C) would look like. The colors used at the tone-color combination (Concert Pitch 440Hz) as described in the Roel’s World article about Sound (Music) & Light (Color).

THE TETRACTYS & MUSICAL INTERVAL RATIOS

The tetractys (Greek: τετρακτύς), or tetrad, or the tetractys of the decad is a triangular figure consisting of ten points arranged in four rows: one, two, three, and four points in each row, which is the geometrical representation of the fourth triangular number.

You can see the Tetractys as a geometric representation of many Just interval ratios (when relating a row to one or more above).

You might have noticed already the Octave 2:1, as well as the Just Fifths (3:2) – the Pythagorean scales are based on the stacking of the Just Fifth – and it’s inversion, the Just Fourth (4:3).

When just looking at the single dot on top, you can “picture” the Tonic or Unison (1:1).

Now, picture the Tetractys to extend beyond the row with 4 dots, with more dots: 5, 6, 7, 8 … et cetera, then we get: 5:4 (Just Major Third), 6:5 (Just Minor Third), 7:6 (Septimal Minor Third), 8:7 (Septimal Major Second), 9:8 (Pythagorean Major Second), 10:9 (Small Just Whole Tone), 11:10 (Neutral Second or “Ptolemy’s Second”), 12:11 (Undecimal Neutral Second), et cetera …

And if you would “skip” a row in the Tetractys, more intervals appear: 3:1 (Just Twelfth), 5:3 (Just Major Sixth), 7:5 (Septimal Tritone), 9:7 (Septimal Major Third), 11:9 (Undecimal Neutral Third), et cetera …

Or “skip” 2 rows and even more intervals appear: 4:1 (Fifteenth or Two Octaves), 7:4 (Harmonic Seventh), 8:5 (Just Minor Sixth), 10:7 (Septimal Tritone), et cetera …

And how about “skipping” 3 rows: 9:5 (Greater Just Minor Seventh), 11:7 (Undecimal Minor Sixth), 15:11 (Undecimal Augmented Fourth / ‘Tritone‘), et cetera …

As you can see, many intervals can be formed by looking at the Tetractys as geometric representation of musical ratios. You can find an extensive list of intervals on Wikipedia where you can find additional ratios that related to the extended Tetractys displayed in this article.

GEOMETRY OF SCALES

A scale is a serie of tones at specific distances (intervals) from each other. The most common tone distances used in scales are semitones (“s” or “h” = half tone) and tones (“T” or “W” = whole tone / 2 semitones), but some scales do include larger intervals like the minor third (m3 = 3 semitones) and Major third (M3 = 4 semitones).

There are many different scales, too many to list them all in this article. Most scales (including the most common Major and Minor scales) are asymmetrical, only a small number of scales are symmetrical. I will only list a few of the most used scales, as well as several (less often used but) symmetrical scales.

When you connect the tones of scales (in sequence), Polygons (with Chromatic Circle) and Polygrams (with Circle of Fifths) appear. With all scales below the tone “C” is represented by the dot on the top):

C MAJOR AND C NATURAL MINOR SCALES

The Major and Minor polygons (or “Greek Modes Polygram) drawn (below) in the Chromatic Circle (CC) are the same shape just tuned, from Major to Minor with 90 degrees clockwise (CC).

Another interesting thing happens when you superimpose both polygons. You can place a “Mirror” where one half of the superimposed shape mirrors the other half.

	C MAJOR (IONIAN)	C MINOR (AEOLIAN)
	T–T–s–T–T–T–s	T–s–T–T–s–T–T	C MAJOR & MINOR SUPERIMPOSED	MIRROR
	W–W–h–W–W–W–h	W–h–W–W–h–W–W
	2-2-1-2-2-2-1	2-1-2-2-1-2-2
C C
The Major and Minor polygrams drawn (below) in the Circle of Fifths (CoF) are turned (Major to Minor) with 90 degrees counterlockwise (CoF).
C o F

The two tones of the circles are not part of the superimposed C Minor and C Major polygons / polygrams are the C♯/D♭ and F♯/G♭. In both scales the intervals formed between those tones and the tonic (C in this case) – respectively a Minor Second and Tritone – are considered the most “dissonant” intervals in the scale.

The Minor Second though is part of the “tone connections” of the polygons / polygrams, as you can see listed below. Interestingly the Major Third does appear in the tone connections of the polygrams / polygons.

TONE	\|	TONE	INTERVALS CC
C	\|	G	Fifth / Fourth
D	\|	F	Minor Third / Major Sixth
D♯/E♭	\|	E	Minor Second / Major Seventh
G♯/A♭	\|	B	Minor Third / Major Sixth
A♯/B♭	\|	A	Minor Second / Major Seventh

GEOMETRY OF THE GREEK MODES

All “Greek Modes” use the same shape polygon as the Major and Minor scales (Chromatic Circle). On the left an image of the IONIAN mode (or Major scale) polygon (with the tone C on top). The polygons of the other Greek Modes can be found by simply rotating the polygon:

the DORIAN mode polygon is rotated 60 degrees (2 semitones) counterclockwise.
the PHRYGIAN mode polygon is rotated 120 degrees (4 semitones) counterclockwise.
the LYDIAN mode polygon is rotated 150 degrees (5 semitones) counterclockwise.
the MIXOLYDIAN mode polygon is rotated 150 degrees (5 semitones) clockwise.
the AEOLIAN (Minor) mode polygon is rotated 90 degrees (3 semitones) clockwise.
the LOCRIAN mode polygon is rotated 30 degrees (1 semitone) clockwise.

You can also say the sequence of Whole (W) and Half (h) tones is “shifting”:

W – W – h – W – W – W – h = Ionian (the Major scale)
W – h – W – W – W – h – W = Dorian
h – W – W – W – h – W – W = Phrygian
W – W – W – h – W – W – h = Lydian
W – W – h – W – W – h – W = Mixolydian
W – h – W – W – h – W – W = Aeolian (the Minor scale)
h – W – W – h – W – W – W = Locrian

The fat W in the list above is the Whole Tone distance between the G and A in the polygon, opposite the D.

The shape of the “Greek Modes Polygon” might look a bit “odd” at first. This changes though, when you turn the Chromatic Circle and the Ionian Mode polygram itself 60 degrees counterclockwise:

SEPTAGON

SEPTAGRAM

SUPERIMPOSED

2 – 1 – 2 – 2 – 2 – 1 – 2

D – C – B – A – G – F – E – D

m3 – M3 – m3 – M3 – m3 – M3 – m3

D – F – A – C – E – G – B – D

5th – 5th – 5th – TT – 5th – 5th – 5th

D – A – E – B – F – C – G – D

All tone connections.

When looking at this polygram now, you see how well “balanced” polygons and polygrams are formed with the Greek Modes.

The “Gemstone” Septagon connects the 7 tones using Minor and Major 2nds.
The red Septagram connects the 7 tones using Minor and Major 3rds.
The purple Septagram connects the 7 tones using 5ths and one Tritone (TT).

The “connected” tones in the images above, are the “white keys” on the piano.

The shape of the red polygon might look familiar to you:

Blog » Music & Geometry 30 — The Sigil of Ameth

Blog » Music & Geometry 31 — The Sigil of Ameth

The non-connected dots in the tone circles above – the “black keys” on the piano – form a pentagon and pentagram:

PENTAGON	PENTAGRAM	PENTA SUPERIMPOSED	ALL SUPERIMPOSED

2 – m3 – 2– m3 – 2 Ab – Bb –Db – Eb – Gb – Ab	4th <> 4th <> 5th > < 4th <> 4th Db – Ab – Eb – Bb – Gb – Db		White Keys (Greek Modes) Black Keys (penta)

The pentagon connects the 5 tones using Major 2nds and Minor 3rds.
The pentagram connects the 5 tones using 4rds (descending) or 5ths (ascending).

THE “SEQUENCE OF FALLING FIFTHS”

The purple Septagram displayed earlier also visualizes another aspect in music as well: the “harmonic progression” or “chord progression“, a succession of musical chords. This chord progression is the foundation of harmony in the Western musical tradition.

The numeral sequence of the falling (descending) Fifths goes as follows:
(4 -) 7 – 3 – 6 – 2 – 5 – 1

Musicians and composers generally prefer using the Roman numerals instead though:
(IV -) VII – III – VI – II – V – I

In C Major we get the following chord sequence:
(F Major -) B diminished – E minor – A minor – D minor – G Major – C Major.

All “steps” in the sequence “lead” to the tonic, the root of the tonality a composition is written in. I’ve put the (IV) in the sequence above between brackets, because the interval between F and B is not a Fifth but a Tritone.

“THE SEQUENCE OF FALLING FOURTHS”

If you place the 4 on the other side of the reversed sequence then we get a perfect sequence of descending Fourths”:
4 – 1 – 5 – 2 – 6 – 3 – 7:
F Major – C Major – G Major – D minor – A minor – E minor – B diminished.

This “Sequence of Falling Fourths” actually appears when you use the RADIAN measure of 57.29577951 degrees when going ’round the Circle of Fourths (or Circle of Fifths in clockwise movement), as Zachary G Covell demonstrates (see image on the right).

Zack writes:

“After 7 times around the circle all four of the 90 degree lines are filled in. The 11th, 22nd, 33rd, and 44th step in the lines placing each one at a new radian of 57.29577951 degrees becomes the axes of the directions at 90 degrees to one another. Only a musician or someone who knows some music theory will see the 4152637 locations. The 4152637 are Harmonic Progression in Music.“

Going around the Circle in 7 times isn’t a “coincidence” either. When stacking (slightly tempered) Fourths / Fifths you will rise 7 octaves before you come across the “same” tone as you started with (but 7 octaves higher) and “close” the circle. I talk about “tempered” Fourths / Fifths in this case, because if you stack Just (perfect) Fourths / Fifths you would slightly ‘overshoot’ the circle with approx. a quartertone (this difference between 12 stacked Perfect 5ths and 7 stacked Octaves is also called the “Pythagorean comma“) and would thus generate a spiral and not close the circle, as demonstrated by Zach.

The 11th, 22th and 44th are Tritones. The 33rd is not (it’s a “Quartertone“), nor are the 55th, 66th, and 77th. But the 88th is, as is the 176th … This is because there are some “doubling sequences” within the harmonic series as well. The most obvious is that of the 1st harmonic (fundamental): 1-2-4-8-16-32-64-et cetera. But, so does the “Tritone” in the harmonic series: 11-22-44-88-176-352-et cetera. The 33rd harmonic (a “Quartertone”) “doubles” as follows: 33-66-132-et cetera, as does the 55th harmonic: 55-110-220-et cetera … you see the “system of doubles” within the harmonic series, right?

For the “number fetishists” and philosophers among us:

The numerologists among you might have noticed the 11, 22, 33 and 44 series, the so called “Master Numbers” (although not all numerologists use 44).

These numbers are also the first 4 double digit palindromic numbers, numbers that remains the same when its digits are reversed. The Circle of Fifths can be used both ways, the interval stays the same only the direction changes, ascending (clockwise) vs. descending (counterclockwise) 5th.

In the Bible the numbers 11 and 22 symbolize disorder, chaos and judgment. The Tritone is commonly experienced as the most “dissonant” or “tensionful” in the 12-Tone system. 33 represents “God’s Jugement”.
If you count from the 1st line drawn in the circle, the 33rd Harmonic becomes the last “leg” of the cross and the beginning of the last “sequence” (of 4) to close the circle/cycle.
In the Bible a 44 day period began on the day Jesus was crucified and ended with his resurrection. When you look at the circle, the 44th harmonic completes / ends the circle/cycle. It “ends” the “period” between “crucifixion” (33rd Harmonic) and 44th Harmonic.

I know these things don’t have much to do with math or geometry, but are fun nonetheless. *wink*

GEOMETRY OF SYMMETRICAL SCALES

In music, a symmetric scale is a music scale which equally divides the octave. The concept and term appears to have been introduced by Joseph Schillinger and further developed by Nicolas Slonimsky as part of his famous “Repository of Scales and Melodic Patterns“. In 12-tone equal temperament, the octave can only be equally divided into 2, 3, 4, 6 or 12 tone-spaces, which consequently may be filled in by adding the same exact interval or sequence of intervals to each resulting note (called “interpolation of notes”).

EQUALLY SPACED SCALES

CHROMATIC SCALE at CC	CHROMATIC SCALE at CoF	HEXATONiC SCALE at CC & CoF
s–s–s–s–s–s–s–s–s–s–s	s–s–s–s–s–s–s–s–s–s–s	T–T–T–T–T
1-1-1-1-1-1-1-1-1-1-1	1-1-1-1-1-1-1-1-1-1-1	2-2-2-2-2

MIRRORED SCALES

These 7-tone scales – when split in the middle – are mirrored on both sides of the center interval:

	C NEOPOLITAN	C DORIAN	C MAJOR-MINOR	C DOUBLE HARMONIC
	s–T–T – T – T–T–s	T–s–T – T – T–s–T	T–T–s – T – s–T–T	s–m3–s – T – s–m3–s
	1-2-2 – 2 – 2-2-1	2-1-2 – 2 – 2-1-2	2-2-1 – 2 – 1-2-2	1-3-1 – 2 – 1-3-1
C C
C o F

A few notes about the scales above:

The (modern) Dorian scale isn’t the only Greek mode with perfect symmetry (all Greek modes use the same shape polygon), but it’s “turned” so that the top of the “gemstone” polygon and the C on top of the Tone Circles align. The Dorian scale was traditionally the “1st mode” till the Ionian scale was added.
The “Major-Minor” scale (a Heptatonic scale) is actually the natural minor (Aeolian) scale but with a Major 3rd instead of a minor 3rd.
The Double Harmonic scale is also know as the “Arabic”, “Gypsy Major” or “Byzantine” scale. This scale contains a minor 2nd, major 3rd, perfect 4th and 5th, minor 6th, major 7th.

SCALES WITH REPEATING SEQUENCES

These scales – that “split” the octave in 2 – display the same sequence of intervals on both sides of the middle, except for the Augmented Scale that splits the octave in 3:

	C TRITONE	C 2-SEMITONE TRITONE	C DIMINISHED *	C AUGMENTED *
	s–m3–T – s–m3–T	s–s–M3 – s–s–M3	T–s – T–s – T–s – T–s	m3–s – m3–s – m3–s
	1-3-2 – 1-3-2	1-1-4 – 1-1-4	2-1 – 2-1 – 2-1 – 2-1	3-1 – 3-1 – 3-1
C C
C o F

* The intervals of the Diminished and Augmented Scale pitch-pairs (2-1) and (3-1) can also be reversed: (1-2) and (1-3) to create the Auxiliary Diminished and Augmented Scales. The Polygons / Polygrams created will be the same, just turned 30 degrees clockwise.

A few notes about the scales above:

The Tritone scales are Hexatonic (6-tone) scales.
The Diminished and scale (also known as “Korsakovian” and “Pijper” scale) are Octatonic (8-tone) scales. The “Auxiliary” Diminished scale is the enharmonic equivalent of the “Petrushka Chord“.
The Augmented scale (used frequently by Jazz saxophonists such as John Coltrane, Oliver Nelson and Michael Brecker) is a Hexatonic scale containing an interlocking combination of two augmented triads a minor third apart.

GEOMETRY OF CHORDS

Just like with scales also chords form geometric shapes. For this article I will only share the shapes and Polygons for C Major and C Minor. These shapes are the same though for all 12 tonalities.

CHROMATIC CIRCLE

C MAJOR (CM)	C MINOR (Cm)	SUPERIMPOSED	MIRROR	12 TONALITIES

CIRCLE OF FIFTHS

C MAJOR (CM)	C MINOR (Cm)	SUPERIMPOSED	MIRROR	12 TONALITIES

Other common chords in all 12 tonalities superimposed (the colored polygons are C-based):

	C dim	C Aug	Cm7	C7	CM7
C C
C o F

As you might have noticed, there are various chords that “generate” the same polygon when the 12 tonalities have been superimposed, like the Cm7 and C7 in both the Circle of Fifths and the Chromatic Circle.

There are of course many more chords variations with additional notes such as for example 4, 6, 9, 11 and more. Perhaps when I have some free time I’ll add some more to this article.

HARMONIC PROGRESSIONS

When you draw a square around the Circle of Fifths and draw lines between the corners of the square, 4 triangles appear. In each triangle we see the chord progressions that belong to the Major tonality in the center of the outer ring, highlighted by the green triangle. Diminished chords are usually not drawn into the tone circle, but to complete the picture I have added it into a 3rd ring in the center.

This concept only works with the Circle of Fifths. It does not work this way with the Chromatic Circle.

The example below is based on C Major, but you could turn the Circle of Fifths in any direction to see the chord progressions for any other Major tonality.

DEGREE	TONE	FUNCTION	CHORD (TRIAD)
1	C	TONIC	C MAJOR
2	D	SUPERTONIC	D MINOR
3	E	MEDIANT	E MINOR
4	F	SUBDOMINANT	F MAJOR
5	G	DOMINANT	G MAJOR
6	A	SUBMEDIANT	A MINOR
7	B	LEADING TONE	B DIMINISHED

A few examples below of the ‘movement’ created by chord progressions:

BLUES PROGRESSION

A standard Blues uses the 1st, 4rd and 5th degrees:
I → IV → I → V → (IV) → I

TURNAROUND

A standard turnaround uses the 1st, 2nd, 3rd, 5th and 6th degrees:
III → VI → II → V → I

A turnaround creates a “z-like” patern, from the inner ring to the outer ring.

See how the movement between the chords of a standard Blues takes place in the outer ring.

“AUTUMN LEAVES” PROGRESSION & THE GEOMETRY OF THE AUTUMN EQUINOX

When you “map” the chord progressions of some compositions using the Circle of Fifths, geometric shapes may appear as well. Robert Aguirre discovered a very interesting one, relating the Jazz standard “Autumn Leaves” with the Autumn Equinox:

“Since you went away the days grow long … And soon I’ll hear old winter’s song …“

POLAR HARMONY – CHANGING “POLARITY” (“NEGATIVE HARMONY”)

The following images are based on a concept shared by Ernest Levy (writer of “A Theory of Harmony“) where every chord has a “reflection”, a “polar opposite” chord within that key center, created by rotating every single tone around the axes of that key center. With other words, with this concept you can substitute a chord by changing it’s “polarity”. Some musicians refer to this method as “Negative Harmony”. The mirror “reflection” is representative of the reflective qualities between the harmonic and subharmonic series, (“otonality & utonality“).

In this concept the axes between the tonal center (root) and Fifth (the interval between the second and third harmonics, generally considered as the most important and consonant interval) is used to “mirror” chords and scales.

A simple way to visualize it is to “mirror” the chord in the Tone Circle.

In the first image you see the polygon of G7 and the the tonic of C. In order to create the “mirror” in the Chromatic Circle you need to draw a line between the tonics of the G7 and C chords and add perpendicular to this G – C axis the “mirror” (image 2). In image 3 you see the mirrored polygram of G7, that turns out to be a F Minor 6 (as noted in the 4th image).

	G7 – C	ADD AXIS & MIRROR	MIRROR G7	Fm6 – C
C C
	The process is pretty much the same with the Circle of Fifths, except that you add the “mirror” directly in between the tonic and fifth of the tone center:
C o F

Substituting G7 with Fm6 is changing the direction of approach to resolve at C. G to C is a Descending Fifth, F to C an Ascending Fifth. The F Minor 6 chord could also be seen / notated as a D7^b5 chord, but it will not “accentuate” the dominant function as traditionally with G7 or alternatively it’s “reflection” Fm6.

Famous musicians like saxophonist Steve Coleman (interesting read: Symmetrical Movement Concept) and Herbie Hancock have used “Negative Harmony” in their music. This subject gained most “exposure” and “popularity” due to Youtube videos by/with Jacob Collier.

TONNETZ GRID

Another way to visualize (and perhaps easier way to “map” the “polar conversion” of) a chord, is by using the Tonnetz Grid. In musical tuning and harmony, the Tonnetz Grid (German for tone-network) is a conceptual lattice diagram representing tonal space first described by Leonhard Euler in 1739.

This way of visualizing “negative harmony” can be found in detail at this imgur post. For this Roel’s World article I will only show you the example as described above with G7 and C. I’ll use a Tonnetz Grid image by Jan Ott for it:

Blog » Music & Geometry 94 — Polar or Negative Harmonics – Tonnetz Grid

As you might have noticed, the in the Tonnetz Grid “connected” tones on the horizontal lines are a 5th apart. The tones connected diagonally from left-top to right-bottom are a Minor 3rd apart, the tones connected diagonally from bottom-left to top-right are a Major 3rd apart.

NEO-RIEMANNIAN TONNETZ TORUS

An interesting variation of the Tonnetz Grid shown above, is the Torus (or Donut-) shaped Neo-Riemannian Tonnetz Torus.

The red lines connect notes that are a Major Third (and Minor Sixth) apart.

The green lines connect notes that are a Minor Third (and Major Sixth) apart.

The blue lines connect notes that are a Perfect Fifth / Perfect Fourth apart.

With tose 3 lines (one of each color) triangles can be formed. These triangles represent either Major (red–green–blue / RGB) or Minor (green–red–blue) Triad (3-tone) Chords.

GEOMETRY OF RHYTHM

So far in this article we have looked at the geometric relationships between tone (pitch) and geometric shapes (polygons and polygrams). Music though is more then tones alone. An important aspect of music is rhythm and just as with tones, polygons can be used to visualize rhythm.

How does this work?

Well a circle could be divided in any kind of time signatures. You could divide a circle into 4 (standard ‘4/4 time’) or into 3 (‘3/4 time’ – Waltz), into 5 (or ‘5/4 time’ – best known from Dave Brubeck’s “Take Five“), into 7 (‘7/8 time’ – Balkan rhythm), or what ever division you wish to use.

On the left you see a division of a circle into 32 parts (4-8-16-32). This can be used for ‘4/4 time’ musical pieces.

You could draw various standard geometric shapes like for example squares, triangles, lines, hexagons, hexagrams, et cetera.

That though will “limit” the rhythmic options you have. Small adjustments in standard shapes could turn a “static” groove into something more irregular or a groove that swings or shuffles …

STANDARD ‘4/4 TIME’ MEASURE – EXAMPLE 1:

In this example on the left you see 3 geometric shapes:

1 5-sided uneven polygon, 1 dodecagon and 1 line.

The blue uneven 5-sided polygon visualized the kick drum, the yellow dodecagon visualizes the closed hi-hat and the red line visualizes the snare on the 2 and 4.

Kick

♪

𝄽

♪

𝄾

𝄿

Snr

𝄽

♩

𝄽

♩

Hat

♬

STANDARD ‘4/4 TIME’ MEASURE – EXAMPLE 2:

In the example on the left you see 4 geometric shapes:

1 line, 1 blue square, 1 green square and 1 polygon with 12 uneven sides.

The blue square visualizes the kick drum in a so called “Four on the Floor” pattern (common for Disco and House music), the green square visualizes the open hi-hat, the yellow uneven-sided polygon visualized the closed hi-hat and the red line visualizes the snare on the 2 and 4.

Kick

♩

Snr

𝄽

♩

𝄽

♩

OHat

𝄾

𝄿

𝄾

𝄿

𝄾

𝄿

𝄾

𝄿

CHat

♬

𝄿

♬

𝄿

♬

𝄿

♬

𝄿

These were just two very simple examples, but you could make these patterns as complicated as you wish.

XRONOMORPH

The absolute coolest free software you can use for turning geometric shapes into rhythm is called “XronoMorph”.

“XronoMorph is a free OS X and Windows app for creating multilayered rhythmic and melodic loops (hockets). Each rhythmic layer is visualized as a polygon inscribed in a circle, and each polygon can be constructed according to two different mathematical principles: perfect balance and well-formedness (aka MOS). These principles generalize polyrhythms, additive, and Euclidean rhythms. Furthermore, rhythms can be smoothly morphed between, and irrational rhythms with no regular pulse can also be easily constructed.

Each polygon can play an independent sound, and XronoMorph comes with a useful selection of samples to play the rhythms. Alternatively, you can load your own VST or AU plugins, or send MIDI to an external software or hardware synth. The rhythmic loops can be saved as presets within XronoMorph; they can also be saved as Scala scale tuning files, which means XronoMorph can be used as a tool for designing well-formed (MOS) and perfectly balanced microtonal scales.”

Watch the following videos to get a better idea about what you can do with this amazing software:

https://www.youtube.com/watch?list=PLsrqTVnoUqolF-bpvPKJzqMy8Cyzukj3S&v=FgzLRzIM8rc

XronoMorph: An Introduction (https://www.youtube.com/watch?list=PLsrqTVnoUqolF-bpvPKJzqMy8Cyzukj3S&v=FgzLRzIM8rc)

You can download XronoMorph for free from: www.dynamictonality.com

THE COLTRANE CIRCLE

An interesting variant to the “Circle of Fifths” is the “Coltrane Circle”, created by saxophonist John Coltrane (perhaps based on Nicolas Slominksy’s Thesaurus of scales and musical patterns?) and was used by Yusef Lateef for his work “Repository of Scales and Melodic Patterns“.

Being a saxophonist myself and a fan of Coltrane’s work I had no choice then to write something about this tone circle in this article as well.

Below on the left you see a scanned copy of an original drawing of the “Coltrane Circle”. I have modified an image made Corey Mwamba from his article “Coltrane’s Way Of Seeing” that clarifies the scanned image (right image).

In the hand drawing there are a couple of sharps notated, they have been replaced by Corey Mwamba with their enharmonic equivalents (C♯ = D♭ and F♯ = G♭) in his drawings.

A Pentagram & Pentagon appear when you draw lines between the same tones in the Coltrane Circle” (in this example with the tone C).

Note: if the lines, numbers and the Pentagram in the Coltrane Circle (on the left) were drawn by John Coltrane himself is not clear.

There is yet another interesting polygon to be drawn.

In the original drawing Coltrane had “circled”. specific tones. If you connect the circled tones a dodecagram is formed.

NOTE: There is a lot more that can be said about the Coltrane Circle as well as the geometric relationships between chords and chord progressions in some of his music, in particular the album Giant Steps. If you like to know more about this, then read this Roel’s World article: “The Coltrane Tone Circle“.

TORUS KNOT TONE CIRCLE

I came across this interesting-looking Tone Cirle in the shape of a torus knot online. It’s a bit different then the other tone-circles shared in this article but it is an interesting (pretty) concept nonetheless, so I’ll share it here.

If we start from C and follow the strand from “0” to “1” to either side and move to “0” outwards again then we have moved a semitone up or down the scale and end up at C♯ or B. Et cetera …

⟲	STEPS ON STRANDS	⟳
Major 7nd	0 ⇠ 1 ⇠ 0 ⇢ 1 ⇢ 0	Minor 2nd
Minor 7nd	0 ⇠ 2 ⇠ 0 ⇢ 2 ⇢ 0	Major 2nd
Major 6th	0 ⇠ 3 ⇠ 0 ⇢ 3 ⇢ 0	Minor 3rd
Minor 6th	0 ⇠ 4 ⇠ 0 ⇢ 4 ⇢ 0	Major 3rd
5th	0 ⇠ 5 ⇠ 0 ⇢ 5 ⇢ 0	4th
Tritone	0 ⇠ 6 ⇠ 0 ⇢ 6 ⇢ 0	Tritone
4th	0 ⇠ 7 ⇠ 0 ⇢ 7 ⇢ 0	5th

NOTE: The information about this “tone knot” provided in the source article in question is wrong! The writer calls this “tone knot” a “Circle of Fifths” instead of a “Chromatic Circle“. Of course one could assign the Circle of Fifths to the Torus Knot as well, but that is not what we see in the image provided. The writer also calls the Fourths and Fifths “Major“, but Fifths and Fourths are neither Major nor minor.

TONES, ASTROLOGY & GEOMETRY

If you know a little about astrology, then you must have recognized some of the geometric shapes used in the tone circles earlier in this article, in particular those of the intervals. The tone circles might have also reminded you of the way the Zodiac Circle is draw.

Note: The Zodiac Signs in this article are placed clockwise and with Aries “on top”. Traditionally the Zodiac Signs are drawn counterclockwise with Aries on the left. Another difference is that the “cusps” (the line in between the signs) traditionally align with North, South, East and West.

Both tone circles though are drawn as traditionally used, thus turning the Zodiac Circle to match both tone circles (music is the main subject of this article after all) seemed to be more convenient reading and comparing the tone circles with the Zodiac Circle.

	LINE	TRIGON	SQUARE	HEXAGON	DODECAGON	DODECAGRAM

	6{2}	4{3}	3{4}	2{6}	t{6}	t{6/5}={12/5}
C C	TRITONES	MAJOR THIRDS	MINOR THIRDS	MAJOR SECOND	MINOR SECOND MAJOR SEVENTH	FIFTHS FOURTHS
C o F	TRITONES	MINOR SIXTHS	MAJOR SIXTHS	MINOR SEVENTH	FIFTHS FOURTHS	MINOR SECOND MAJOR SEVENTH
	Opposition	Trine	Square	Sextile	Semi-Sextile	Quincunx

	180°	120°	90°	60°	30°	150°
	“POLARITIES“ Opposition	“TRIPLICITIES“ Fire Earth Air Water	“QUADRUPLICITIES“ Cardinal Fixed Mutable	“DUALITIES“ Masculine Feminine

The degrees listed above relate to the angles of 2 dots relatively to each other from the center point of the geometric shapes..

Read more about music, astrology and “Tone Zodiacs” in the article “Zodiac Signs & Tonality (Music)“.

“COUNTING CORNERS”

Another way to look at geometry and sound is angles (arc minutes) and the tones you could generate with them if you change the unit from degrees to Hertz:

POLYGON	ANGLES		ANGLE DEGREE		DEGREE TO HERTZ	HARMONIC
TRIGON	3	x	60°	=	180	1st
QUADRAGON	4	x	90°	=	360	2nd
HEXAGON	6	x	120°	=	720	4rd
DODECAGON	12	x	150°	=	1800	10th

The sum of the angles of these polygons could create the tone of F♯ at 180Hz, 360Hz, 720Hz and 1800Hz.

Other polygons – not found in the standard tone circles – would also create interesting tones. For example, the Pentagram (5 angles of 108°) would generate a C♯ a harmonic 5th at above 180Hz, a Septagon (7 angles of 128 4/7°) would generate an A♯ at 900Hz, the Octagon (8 angles of 135°) generating a C♯ at 1080Hz, et cetera …

With other words, the “series” of Polygons with increasing number of angles relates closely to the Harmonic Series in music.

Of course Hertz and Degrees is not the same thing. Most sound frequencies are ‘directional’ and/or ‘omni-directional’. No ‘sharp edges’ as with a triangle or square, but spherical and/or cone-shaped.

You can’t just “swap” units and say it’s all the same. But there does seem to be a lot of similarities between the math behind the units, as between many things in the universe. Some ‘laws’ seem to apply for a lot of things if not everything.

3 DIMENSIONAL REPRESENTATION

Some authors have taking mapping tone relationships one step further, turning the more “traditional” 2D Polygons into 3D shapes. At the website www.cosmometry.net for example Marshall Lefferts converted the 2D Circle of Fifths into a 3D Vector Equilibrium.

Marshall Lefferts writes: “This illustration shows that the tri-tone intervals are exactly opposite each other in the circle of fifths”. [left]
“In this way we can easily see the six pairs of opposite notes that comprise the basic 12-tone system of music.”

“Extending this into the 3-dimensional space of the vector equilibrium, one of the primary components of cosmometry, we can map these pairs like this (notice that the circle of fifths is maintained in the sequence of notes as they are arrayed visually around the center).” [image right]

“Buckminster Fuller stated that the vector equilibrium is composed of six-pairs of equal and opposite vectors radiating from its center point. The music system aligns with that model conceptually, though of course the frequency differences of the actual tri-tone notes are not equal.”

Instead of blogging more about the 3 dimensional representations of musical harmony and tone-relationships it might be more useful to share some very interesting videos made by others with you:

PLATONIC SOLIDS

We can’t call this geometry article “complete” without mentioning the Platonic Solids.

The reason to mention these is because of their obvious relation with a few of the shapes found earlier in this article, in particular the Trigon (triangle) and Quadragon (Square).

The Platonic Solid that is a direct “one-on-one” match with musical geometry is the Tetrahedron. You can create a Tetrahedron by connecting 4 Trigons (the Major Thirds / Minor Sixths relationships within one octave within the tone circle).

For the Octahedron you would need 2 2/3 octaves, and 5 octaves for the Icosahedron.

The 3 Squares that represent the Minor Thirds and Major Sixths relationship within the tone circle only forms half a Hexahedron. You would need to cover 2 octaves to generate 6 Squares to complete the Hexahedron.

The only Platonic Solid that does not relate to the polygons created within the standard tone circle is the Dodecahedron, only in the Coltrane circle we could draw a Pentagon (and Pentagram).

Also interesting are the Schäfli Symbols {corners of the polygon shape of a face, edges connected to the corners}. Their recursive definition (or inductive definition) look similar to several tone interval ratios:

POLYHEDRON		SCHLÄFLI	AS RATIO	INTERVAL
	Tetrahedron	{3, 3}	3:3 = 1:1	UNISON
	Hexahedron (Cube)	{4, 3}	4:3	PERFECT 4TH
	Octahedron	{3, 4}	3:4 (3:2·2)	PERFECT 5TH
	Dodecahedron	{5, 3}	5:3	JUST MAJOR SIXT
	Icosahedron	{3, 5}	3:5 (2·3:5)	JUST MINOR THIRD

“For the Pythagoreans and later Greek philosophers, tetrachords were considered to be the auditory geometry of a “perfect” 4-sided, 4-pointed tetrahedron solid. As a geometrical model for music, the two tetrachords in a Greek mode could have been intended to represent two opposing and interlocking tetrahedrons balanced around a shared center, thereby creating the 8 vertices of a cube or hexahedron. Alternatively, the vertices (or points) of this cube could have also been intended to pinpoint the center of 8 triangular faces that form its geometric opposite, the octahedron.

In either case, the geometric perfection represented by two balanced tetrachords is the founding principle behind the Greek modes and thus even our present major and minor system of scales.

Greek geometers found that tetrahedrons could be used to construct more complex perfect shapes. For example, a pair of octahedrons can be balanced to form either the 12 vertices of an icosahedron or 12 pentagonal faces of a dodecahedron. Because of this, tetrachords, octaves and a stack of twelve perfect 5ths were associated with the geometrical shapes of the five perfect solids, which the Greeks considered integral to the structure of the universe.“

From: “Interference – A grand scientific Musical Theory” by Rich Merrick (www.interferencetheory.com)

For creating a 12-Tone Tetrahedron you need to combine 4 (2D) Trigons.

1 Trigon is formed by the (3) tones of an Augmented Triad (C-E-Ab, Eb-G-B, Gb-Bb-D and Db-F-A).

Each trigon shifts a semitone up or down at the corners with the neighboring trigons.

8-TONE (MAJOR SCALE) MERKABA

Merkaba is a combination of three different words. Mer is a light that rotates within itself; Kameant refers to the human spirit and Ba alludes to the physical human form (body).

A Merkaba is a star tetrahedron, a three dimensional 8 pointed star made from 2 tetrahedrons, one pointing up and the other down.

The Merkaba harmonizes male and female energy, much like a Yin/Yang symbol and is a representational invocation of “as above, so below”. The pyramid pointing upwards connects us to heavenly universal energy and represents yang, positive energy flows. The pyramid pointing downward connects to the earth and resonates with yin, negative energy flows.

The first “Tone Merkaba” I came across was the drawing below by Druvalo Melchizedek from his book “The Ancient Secret of the Flower of Life”.

In his Tone-Merkaba Druvalo Melchizedek places the tones at the vertexes of the Merkaba based on the Major scale, connecting 2 groups of 4 tones (tetrachord) with 8 vertexes.

He starts at the female tetrahedron (point down) with Do (1) – whole tone to – Re (2) – whole tone to – Mi (3) – half tone to – Fa (4), scale degrees 1-2-3-4. At Fa he “crosses over” (with one whole tone) diagonally from one Tetrahedron to the other, the male tetrahedron (point up) and continues there with the same pattern of whole, whole, half tone: Sol (5) – whole tone to – La (6) – whole tone to – Si (7) – half tone to – Do (8), scale degrees 5-6-7-8.

In his concept the semitone leads to the vertex that changes the “polarity” (female to male and visa versa) when diagonally “crossing over”: Fa (4) to Sol (5) and Do (8) to Do (1).

Even though a very interesting concept, I wondered if there would be a different way to align the tones with the Merkaba. The “As Above, So Below” aspect of the Merkaba is not very clear with the way Melchizedek aligned the tones.

AS ABOVE, SO BELOW

If you haven’t read the Roel’s World article “The Functions of the Intervals” then that might be helpful to read first.

If we draw a line through the center located of the Merkaba, then 4 tones are located below the middle and 4 above (image left below).

Interesting is that when drawing lines from the vertexes through the center of the Merkaba, the opposing vertexes are each others inversions if you look at the scale degrees: 1↔8 (Tonic & Octave), 2↔7, (Seconds and Sevens), 3↔6 (Thirds and Sixes) and 4↔5. (Fourths and Fifths). And in all cases the degree of the connected vertexes combined generates the number 9 (number of completion).

Another interesting thing about this way of aligning the tones as displayed above, is that both horizontal planes of the tetrahedrons “rotate” in opposite direction 2→3→4 (clockwise) and 5→6→7 (counterclockwise).

If you would look at it from the point of the “Do’s” in 2D perspective, then the male “Do” (8) is grouped with 3 surrounding female tones: Re (2) – Mi (3) – Fa (4) and the female “Do” (1) is grouped with 3 surrounding male tones: Sol (5) – La (6) – Si (7).

This reminded me a little of the Yin-Yang symbol, where a dot of the opposite gender is located in the center of each half.

HUMAN VOCAL RANGE

There is yet another way to associate the 8 tones of the Major scale with the 8 vertexes of the Merkaba, this relationship is based on the human vocal ranges. The human vocal range is divided into 6 ranges, 3 female ranges, 3 male ranges, based on the everage vocal range of respectively women and men. From high (female) to low (male) these ranges are:

Female – Soprano: C4 – C6
Female – Mezz. Sopr: A3 – A5
Female – Cont. Alto: F3 – E5

Female: C-A-F (ascending 6ths / descending 3rds)
or inverted F-A-C (ascending 3rds)

Male – Tenor: B2 – A4
Male – Baritone: G2 – F4
Male – Bass: E2 – E4

Male: B-G-E (ascending 6ths / descending 3rds)
or inverted E-G-B (ascending 3rds).

To turn these 3-tone chords into 2 4-tone chords we have to add one tone to each group.

The Female group does have a C / Do (1) already, so the second Do (8 – Octave) has to be added to the Male group: D-F-A-C (a Dmin7 chord), scale degrees: 2-4-6-8 (even numbers).

The only tone of the C Major Scale that is missing, is the tone D / Re (2). When we add this tone to the Female group we get the following group (chord): C-E-G-B (a CMaj7 chord), scale degrees: 1-3-5-7 (uneven numbers).

What version of the Tone-Merkaba you should use (Druvalo Melchizedek’s Tone-Merkaba, the “As Above, So Below” Tone-Merkaba or the Tone-Merkaba based on the human vocal range) is up to you.

MAPPING NUMBER SEQUENCES

You could also generate interesting looking polygons/polygrams by mapping mathematical sequences onto the Chromatic Circle and the Circle of Fifths. You could map practically any series of numbers, you could use your own birthday, telephone number, numerological character values of a word or what ever you feel like.

In the examples below I use semitones, every number in the sequence represents the number of semitones I go up the chromatic scale. The number “0” does represent nil movement around the circle.

You could of course also chose to use whole tones instead (the amount of semitones up the scale then becomes the number from the sequence x 2) or any other progression if intervals if you wish.

In the examples below I stop mapping when I doubled a tone. Of course you could also continue mapping until you have connected all 12 tones …

PI 3.14159265 from C
For this example we use the first 9 digits of Pi. We start at C and go the number of semitones up as follows in the 8-tone (plus octave) sequence:

C +3 D♯ +1 E +4 G♯ +1 A +5 D +9 B +2 C♯ +6 G +5 C

PHI 1.61803 from C
For this example we use the first 6 digits of Phi. We start at C and go the number of semitones up as follows in the 5-tone / (pentatonic) scale (plus octave) sequence:

C +1 C♯ +6 G +1 G♯ +8 E +0, +5 C

Fibonacci Sequence: 0, 1, 1, 2, 3, 5 from C
For this example we use the first 6 digits of the Fibonacci Sequence. We start at C and go the number of semitones up as follows in the 5-tone / (pentatonic) scale (plus octave) sequence:

C +0, +1 C♯ +1 D +2 E +3 G +5 C

If you like to read more about music and number sequences, then check “Music Composition & Math (numbers)“.

REFERENCES MENTIONED IN THIS ARTICLE:

Wikipedia (articles about: Pi, Phi, Fibonacci, and other).
www.cosmometry.net by Marshall Lefferts
“Coltrane’s Way Of Seeing” by Corey Mwamba

Books mentioned and/or quoted from in this article and other related books: