RENOLD-I TEMPERAMENT (“THE SCALE OF FIFTHS”)
I came across the “Twelve True-Fifths Tuning” concept (by Maria Renold) through a facebook friend, Brain T. Collins, who mentioned this tuning concept on his web site, the Omega432.com. Brian T. Collins refers to the page of Graham H Jackson where the “Twelve True-Fifths Tuning” concept is explained. This concept is a great alternative implementation of the Pythagorean Temperament.
NOTES:
- The frequencies listed in this blog article are the result of the original “Scale of Fifths” tuning method (discovered in 1962), also referred to as “Renold I” Temperament. Maria Renold later found out that Henricus Grammateus had constructed a similar scale in 1518 (source: Jorgensen, 1991, p.332).
- In her work Maria Renold used alternative names for the black keys of the piano. C#/Db = “delis“, D#/Eb =”elis“, F#/Gb = “gelis“, G#/Ab = “alis” and A#/Bb = “belis“. For this article I will use the common tone names instead.
- Maria Renold did continue experimenting and developing her concept, with the “Renold II” (also known as “Middle Tuning” temperament as result. This Renold-II temperament is described in the article Renold-II Temperament.
WHY AN ALTERNATIVE FOR THE PYTHAGOREAN TEMPERAMENT?
Well, the Pythagorean Temperament works with the stacking of perfect fifths. But, when we stack 12 perfect fifths, we do not end up at a the same note we started, but approximately a quarter-tone above. With other words, we don’t end up with a circle but a spiral. This actually happens with any perfect (pure, natural) interval (except for the octave) when stacked (and that does not work very well with a closed musical interval system). In order to close the circle, one or more 5th’s should be slightly decreased to end up with a perfect circle. Maria Renold though came up with an tempered version of the Pythagorean Temperament, using mostly Perfect Fifths and still create a working closed circle.
Graham H. Jackson explains on his site:
“For the “twelve true-5ths tuning”: you first set C at 256 Hz. Then you tune the 7 “white keys” by the circle of 5ths, using however natural 5ths. Then you divide the octave at C exactly in half (which can be done handily with a special tuning fork), and tune the 5 “black keys” by natural 5ths to that F#.
You end up with two series of natural 5ths: one of 7 notes, and one of 5 notes, linked by an “unnatural” interval of an augmented 4th (which is actually the same augmented 4th found in the equal-tempered system).“
SO, HOW DOES THAT WORK?
We know that the perfect fifth uses the ratio 3:2. We use the following formula for calculating the fifth:
Frequency • 3 / 2 = Frequency of the Fifth above.
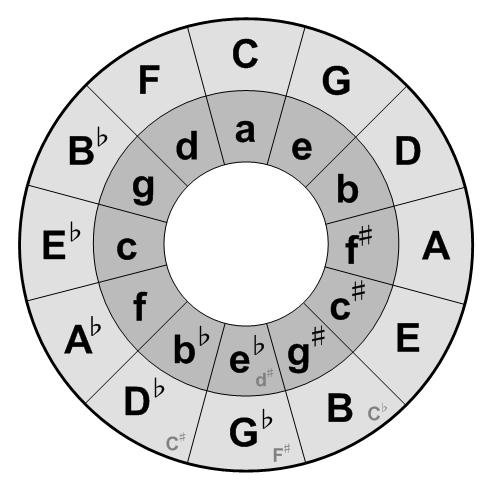 Now, let’s have a look at the Circle of Fifths:
Now, let’s have a look at the Circle of Fifths:
When we follow the Circle clockwise, we go up a fifth. The outer “ring” with the capital letters is the Major Circle of Fifth, with inside the parallel minor Circle of Fifths.
As suggested by Graham H. Jackson, we start with from the tonic of the the C Major scale (the white keys on the piano). Now, the C Major scale contains the following tones: C – D – E – F – G – A – B.
When we start with C3=128Hz (as Renold suggested) and implement the formula we get the following:
128 (C3) • 3 / 2 = 192 (G3) • 3 / 2 = 288 (D4) • 3 / 2 = 432 (A4) • 3 / 2 = 648 (E5) • 3 / 2 = 972 (B5).
In this article I will use the tone frequencies between C4=256Hz and C5=512Hz so it will be easier to “compare” to the
tone frequencies on the modern standard.
256 (C4) • 3 / 2 = 384 (G4) • 3 / 2 = 576 (D5) • 3 / 2 = 864 (A5) • 3 / 2 = 1296 (E6) • 3 / 2 = 1944 (B6).
!IMPORTANT:
If we continue stacking 5ths (• 3 / 2) after B6 (1944Hz), we pass Gb, Db, Ab, Eb and Bb, ending up with F10=22143.375Hz. If we would stack another 5th on top, we end up at C11=33215.0625Hz.
!!! A perfect C11 relative to C4=256Hz would be C11=32768Hz, not C11=33215.0625Hz !!!
With other words, the fifth between F10 and C11 would be imperfect. If we bring that F10=22143.375Hz back to F4, we will end up with 345.990234375Hz. This is about 4Hz higher then the “harmonic mean”. So, we have to use a different method, to get the harmonic mean right. This is where mathematical formulas can help us out.
CALCULATING THE ARITHMETIC, GEOMETRIC AND HARMONIC MEANS
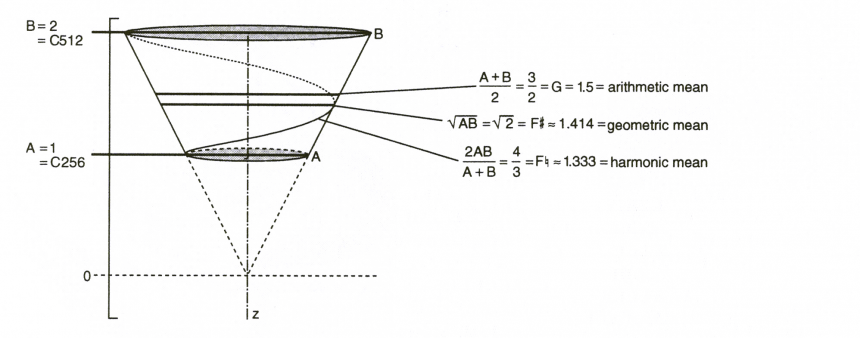
When we calculate the means in between C4 = 256Hz and C5 = 512Hz we get the following
The arithmetical mean formula: (256 + 512) / 2 = 384Hz (G, the 5th above C).
The geometrical mean formula: √ (256 • 512) = 362.038671968Hz (F# or Gb, the dim. 5th above C).
The harmonic mean formula: (2 • 256 • 512) / (256 + 512) = 341.333∞Hz (F, the 4th above C).
The arithmetical mean G = 384Hz was already part of the scale (the first perfect 5th we stacked on the C). Now we have calculated the harmonic mean as well, we can add F = 341.333∞Hz to the scale and we have completed the C Major scale.
| C | D | E | F | G | A | B | C |
| 256 | 288 | 324 | 341.333∞ |
384 | 432 | 486 | 512 |
If we start from the geometrical mean between C4 and C5, the F# (or Gb), stack 5 perfect fifths, and bring them back in between C4-C5, we get the following Major Pentatonic Scale of F# (or Gb):
| F#/Gb | C#/Db | G#/Ab | D#/Eb | A#/Bb |
| 362.039 | 271.529 | 407.294 |
305.470 | 458.205 |
Note: the frequencies noted above are rounded off on 3 digits behind the dot.
When we combine the C Major Scale and the F#/Gb Major Pentatonic Scale, we get the following Chromatic Scale from C:
| C | C#/Db | D | D#/Eb | E | F | F#/Gb | G | G#/Ab | A | A#/Bb | B | C |
| 256 | 271.5 |
288 | 305.5 |
324 | 341.333∞ |
362 |
384 | 407.3 |
432 | 458.2 |
486 | 512 |
In modern music we use only 12 tones. The consequence of this choice is that it is impossible to create a perfect system (a perfect circle of intervals using only perfect intervals), the natural “movement” sound makes when only using perfect intervals is spirally. And you can’t expect to see a spiral if you are drawing a perfect circle right? When we use Maria Renold’s “Scale of Fifths” concept and like to use a closed circle, then we end up with “just another” tempered version of the Pythagorean Temperament.
When we use the tone frequencies as listed above and calculate the amount of cents (rounded off) in between the Fifths, you notice that most intervals are about 0.1 cent off (lower or higher) from the 702 cents of the Perfect Fifth (Just Intonation). There are though two intervals – the Fifths between B and Gb/F# and between Bb/A# and F – that are smaller then the other 10 intervals:
| C | G | D | A | E | B | Gb F# |
Db C# |
Ab G# |
Eb D# |
Bb A# |
F | C |
| 701.9 | 701.9 | 701.9 | 701.9 | 701.9 | 690 | 701.9 | 702.1 | 702.1 | 701.7 | 647.5 | 701.9 |
When we rearrange the circle chromatically we end up with semitones of 101.8-102.1 cents between every semitone, except in between between E-F and B-C, the only two semitone intervals of the Diatonic Scale:
| C | C# Db |
D | D# Eb |
E | F | F# Gb |
G | G# Ab |
A | A# Bb |
B | C |
| 101.8 | 102.1 | 102.1 | 101.9 | 90.2 | 101.8 | 102.1 | 101.9 | 101.9 | 101.9 | 101.9 | 90.2 |
Below a list with the differences in cents and ratio between the Equal Temperament (present standard) and Maria Renold’s “Scale of Fifths” Renold-I Temperament, both using the Scientific Concert Pitch C4=256Hz.
| TONE | 12-TET C4=256Hz | M. R. SCALE OF FIFTHS | CENTS DIFFERENCE | RATIO f2 / f1 DIFFERENCE |
| C4 | 256 Hz | 256 Hz | 0 | 0 |
| C#/Db | 271.2 Hz | 271.5 Hz | 1.9140234664560511 | 1.0011061946902655 |
| D | 287.4 Hz | 288 Hz | 3.6104998468059137 | 1.0020876826722338 |
| D#/Eb | 304.4 Hz | 305.5 Hz | 6.244825443055806 | 1.0036136662286466 |
| E | 322.5 Hz | 324 Hz | 8.033583088810076 | 1.0046511627906978 |
| F | 341.7 Hz | 341.333∞ Hz | -1.858725915674287 | -0.9989269339576626 |
| F#/Gb | 362 Hz | 362 Hz | 0 | 0 |
| G | 383.6 Hz | 384 Hz | 1.8043087084650533 | 1.0010427528675703 |
| G#/Ab | 406.4 Hz | 407.3 Hz | 3.8296946774990657 | 1.002214566929134 |
| A | 430.5 Hz | 432 Hz | 6.021689719949426 | 1.0034843205574913 |
| A#/Bb | 456.1 Hz | 458.2 Hz | 7.952746136304442 | 1.00460425345319 |
| B | 483.3 Hz | 486 Hz | 9.644782878502031 | 1.005586592178771 |
| C5 | 512 Hz | 512 Hz | 0 | 0 |
For tuning by ear three tuning fork are needed: C4=256Hz, A4=432Hz and “gelis” (F#/Gb)=362,04Hz (Renold 1). How to tune by ear is described (scheme included) in Maria Renold’s book
Here an example how the Renold I temperament sounds (in comparison with Equal Temperament):
RENOLD-II
An alternative for the Renold-I Temperament (in particular for acoustic instruments) is the Renold-II Temperament.
DOWNLOADS (MIDI & SOFTSYNTH SCRIPTS)
I have added the “Scale of Fifths” to Scala (a software tool for creating scales, temperaments and more) and exported it in various formats. If you need a different format then provided, download Scala as well as this: SoF – Scala scale.scl scala-file and export it in the format you require.
Note: I do not guarantee the files bellow will work with your hardware and software setup. In case it does not, then try creating and exporting the “Scale of Fifths” yourself with Scala. Please, do feel free to send me a message if the provided files do not work for you, preferably with some info about the hardware, operating system (version) and software you have used.
DOWNLOAD (right-click mouse button: “Safe as”):
- Scala Scale (.scl)
- TUN standard format for softsynths (.tun)
- MIDI Tuning Standard single notes dump (.mid)
- Steinberg Cubase and Nuendo VST microtuner (.xml)
- Roland GS & JV and XP families (.mid)
- Yamaha XG family (.mid)
- Native Instruments Kontakt 2 (via script file)
- Native Instruments Pro-52 and Pro-53 (.p5m)
- Native Instruments Reaktor (via frequency .txt file)
- Native Instruments Reaktor (via .ntf table file)
- Native Instruments Absynth (via .gly file – place in Absynth tuning folder)
- Max Magic Microtuner for Max, MSP and Pluggo (.mtx)
THE BOOK BY MARIA RENOLD
“The Scale Of Twelve Fifths” (and more) can be found in the book “Intervals, Scales, Tones and the Concert Pitch C = 128Hz“. by Maria Renold. Information about “The Scale Of Twelve Fifths” can be found at Chapter 13, 21, 24 & 25 of this book.
 ISBN 9781902636467
ISBN 9781902636467
www.templelodge.com
Why is it that certain intervals, scales and tones sound genuine and others false? Is the modern person able to experience a qualitative difference in a tone’s pitch? If so, what are the implications for modern concert pitch and how instruments of fixed tuning are tuned?
Maria Renold tackles these and many other questions, providing a wealth of scientific data. Her pioneering work is the result of a lifetime’s research into Western music’s Classical Greek origins, as well as a search for new developments in modern times. She strives to deepen musical understanding through Rudolf Steiner’s spiritual-scientific research, and she also elucidates many of Steiner’s often puzzling statements about music.
The results of her work include the following discoveries: that the octave has two sizes (a ‘genuine’ sounding octave is bigger than the ‘perfect’ octave); that there are three sizes of ‘perfect’ fifths; that an underlying ‘form principle’ for all scales can be found; and, most importantly, the discovery of a method of tuning the piano which is more satisfactory than equal temperament. She also gives foundation to some of Rudolf Steiner’s statements such as: ‘c is always prime’ and ‘c = 128 Hz = Sun’.
MARIA RENOLD (1917-2003) spent her childhood in the United States, where her parents emigrated to found a eurythmy school in New York. She studied eurythmy and later violin and viola and toured with the Bush Chamber Orchestra and the Bush String Quartet. One of Maria Renold’s deeply-felt questions concerned the correct concert pitch. When she heard of Rudolf Steiner’s concert pitch suggestion of c = 128 Hz she put it into practice immediately, and experimented with it over many years in America and Europe. She also discovered a new method of tuning the piano, closer to the tuning of stringed instruments, arriving at the concert pitch of a4=432 Hz. First published in German in 1985, her book has become a modern classic of musical research.
REFERENCES:
- Graham H. Jackson (Official web site)
- Omega432.com (a website by Brain T. Collins)
Special thanks to Sławek Kędra providing additional information and suggestions.

