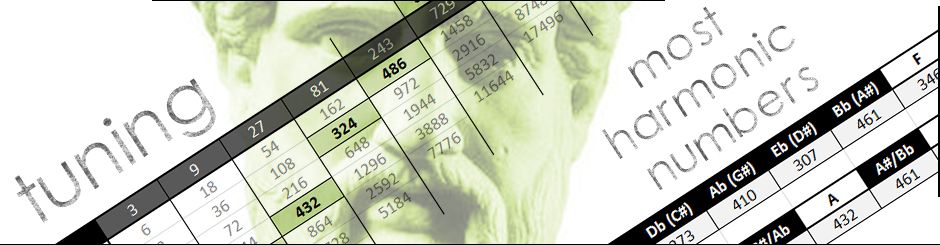
MOST HARMONIC NUMBERS (MHN) CONCEPT, BETTER KNOWN AS THE “PYTHAGOREAN TEMPERAMENT”
The list of frequencies in this document form the Pythagorean Temperament, and have also been shared online as “Most Harmonic Numbers”.
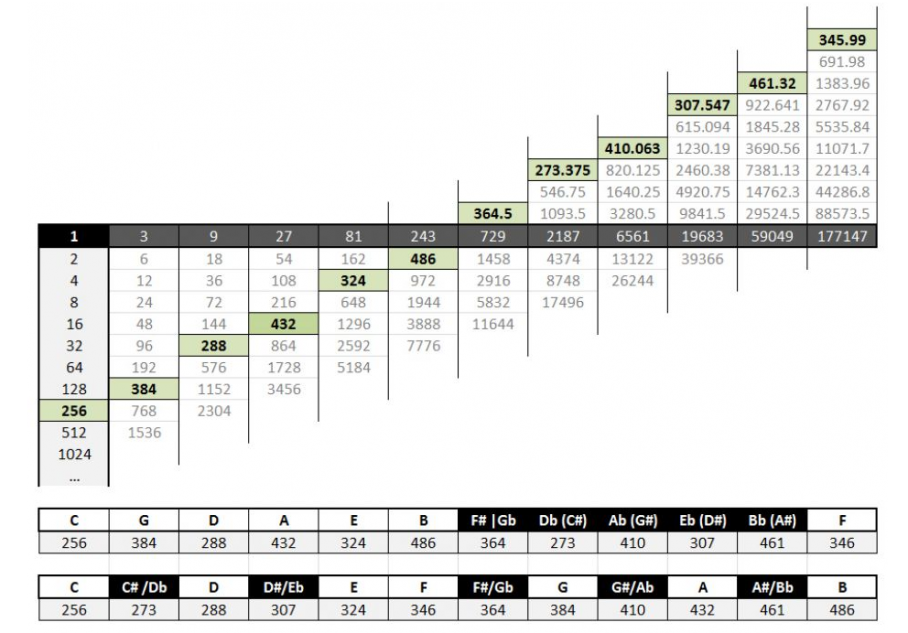
MHN RELATIVE TO TWELVE-TONE EQUAL TEMPERAMENT:
The intervals between the tones when calculated using the Pythagorean Perfect Fifth (ratio 3:2) and those calculated using the 12-TET method are rather different. Below a table that displays the modifications required when using the Most Harmonic Numbers in comparison with 12-TET at Concert Pitch A4=440Hz.
| TONES | HMN FREQUENCY (Hz) | CENT CORRECTION | |
| DO | C | 512 | -37.6312241210787 |
| SI / TI | B | 486 | -27.855595894044 |
| Bb / A# | 461.320 | -18.0837059915098 | |
| LA | A | 432 | -31.7666536334292 |
| Ab / G# | 410.063 | -21.9907990325915 | |
| SOL | G | 384 | -35.6747298650793 |
| Gb / F# | 361.500 | -25.8996731339595 | |
| FA | F | 345.990 | -16.1266721682703 |
| MI | E | 324 | -29.8139799005726 |
| Eb / D# | 307.547 | -20.0360353716339 | |
| RE | D | 288 | -33.7230226885739 |
| Db / C# | 273.375 | -23.948955024014 | |
| DO | C | 256 | -37.6345327289834 |
The cent correction listed above, is the amount of cents (not percents!) difference between the frequencies of the tones according to C4=256Hz (concert pitch) 12-TET (temperament), and what the tones when using the the Most Harmonic Numbers concept should be.
In the table above we find the following columns:
- Solfeggio Syllables (not the “Ancient Solfeggio Frequencies“).
- Tone names.
- Most Harmonic Frequency (between C4 and C5).
- Cent correction (in comparison with 12-TET under concert pitch A4=440Hz).
- A4 Concert Pitch for 12-TET instruments when micro-tuning is not possible, to adjust the first degree (prime / tonic) to it’s most harmonic frequency.
Another way to visualize some of the tones of the “Most Harmonic Numbers” table can be seen in the video by John F. Sase below:
MOST HARMONIC NUMBERS – Scientific Concert Pitch
The MHN-SCP concept is better knows as the “PYTHAGOREAN TEMPERAMENT” and works for instruments that use micro-tuning, as well as fret-less string instruments and trombone (a brass/wind instrument without buttons/tone-holes/pistons), using Concert Pitch C4=256Hz (Scientific Pitch)
“Scientific pitch is an absolute pitch standard that sets middle C (or C4) to 256 Hz. It was introduced in the early 20th century. A4 on this scale is approximately 430.5 Hz, noticeably different from the current concert pitch standard of 440 Hz. It is no longer used by concert orchestras but is still sometimes favoured in scientific writings for the convenience of all the octaves of C being an exact round number in binary counting. The number to the base ten, (256)10, is equal to (100000000)2 to the base two. More usefully, the octaves of C remain a whole number all the way down to 1 Hz (in either counting system).“
— Wikipedia
IF “micro-tuning” is possible with the instruments you use, try to temper (re-tune/pitch) your 12-tone instrument to the following tone-frequencies / cent correction (see colum 3 & 4). Pitching using cents is more accurate then changing the concert pitch using “rounded off” frequencies numbers.
LIMITATIONS OF THE MOST HARMONIC NUMBERS (SCP) CONCEPT:
Since the 432 “Most Harmonic Numbers” is actually knows as “Pythagorean tuning” (Circle of Perfect Fifths), any “limitations” related to the Pythagorean temperament do reflect on this concept as well. There for I will share some information and thoughts about it.
Everyone who knows a bit about temperaments, must have read about the disadvantages of the Pythagorean Temperament. Below some bit’s and pieces of information about the “problems” concerning Pythagorean Tuning.
Pythagorean tuning was a system of just intonation which tuned every note in a scale from a progression of pure perfect fifths. This was quite suitable for much of the harmonic practice until then (See: Quartal harmony), but in the Renaissance, musicians wished to make much more use of Tertian harmony. The major third of Pythagorean tuning differed from a just major third by an amount known as Syntonic comma, which musicians of the time found annoying.
Pythagorean tuning also had a second problem, which Meantone temperament does not solve, which is the problem of modulation, which is restricted because both have a broken circle of fifths. A series of 12 just fifths as in Pythagorean tuning does not return to the original pitch, but rather differs by a Pythagorean comma, which makes that tonal area of the system more or less unusable.
Pythagorean tuning ignores A♭, and uses only the 12 notes from E♭ to G♯. This, as shown above, implies that only eleven just fifths are used to build the entire chromatic scale. The remaining fifth (from G♯ to E♭) is left badly out-of-tune, meaning that any music which combines those two notes is unplayable in this tuning. In the case of Pythagorean tuning, all the fifths are 701.96 cents wide, in the exact ratio 3:2, except the wolf fifth, which is only 678.49 cents wide, nearly a quarter of a semitone flatter.
In meantone temperament, this effect is even more pronounced (the fifth over the break in the circle is known as the Wolf interval, as its intense beating was likened to a “howling”).
If the notes G♯ and E♭ need to be sounded together, the position of the wolf fifth can be changed. For example, a C-based Pythagorean tuning would produce a stack of fifths running from D♭ to F♯, making F♯-D♭ the wolf interval. However, there will always be one wolf fifth in Pythagorean tuning, making it impossible to play in all keys in tune.
Because of the wolf interval, this tuning is rarely used nowadays, although it is thought to have been widespread. In music which does not change key very often, or which is not very harmonically adventurous, the wolf interval is unlikely to be a problem, as not all the possible fifths will be heard in such pieces.
— Wikipedia
As you have read, the circle Pythagoras had in mind, is not perfect, it simply doesn’t close.
If I may quote Richard Merrick (www.interferencetheory.com) from his work “Interference – A Grand Scientific Music Theory”:
“Pythagoras found that pitch follows a logarithmic spiral of frequency into infinity. For example, when the last pitch in stack of twelve perfect 5th intervals is transposed down next to the starting tone, there remains a small gap of about a quartertone.”
Al Leone writes in his work “The Totality of God and the Izunome Cross“:
“When you climb the great pyramid of universal diversity and arrive at its apex, at Unity, at God, you can understand how all we see, and all we can’t, could have come from a single frequency – what Susan Alexjander had noted Dr. Larry Dossey as calling the “Great Tone”. And it is Pythagoras’s Cycle of Fifths that we can again thank for this truth. We saw that when you follow it around to complete the Cycle, you don’t return to where you began.”
ALTERNATIVE
If you think about using the MHN SCP concept / Pythagorean Temperament, then I would like to suggest using a concept developed by Maria Renold, based upon it. Why? Well, the Pythagorean Temperament (and thus the MHN SCP concept) is “flawed” by design: when stacking 12 perfect Fifths you would “overshoot” the Circle of Fifths with about a quartertone, the circle does not close. Maria Renold developed a concept that fixed the issues concerning the “wolf interval”, the “false Fifth”. And thus I would recommend using it instead …
[ Read more ] ►
MOST HARMONIC NUMBERS – Tonic Concert Pitch
The MHN-TCP variation is for 12-TET instruments. These instruments are (for example) fretted string instruments and some keyboards / synthesizers, wind instruments and others. This “concept” can also be implemented in post production when working with instruments that can not change temperament. This method is an simplified implementation of the “Movable Do” system, using the “Do” (first degree, the tonic, of a scale) as tuning reference. This way you can still use one of the 12 “Most Harmonic Numbers” as pitch reference.
EXAMPLE: When a piece is written in A (major or minor), the tonic is the A, there for A4=432Hz. But, if a piece in C (major or minor) then C – the tonic – should be C=256Hz, there for (when using 12-TET instruments) 430.5Hz (-37.631… cent).
- Even though the tonic (movable-DO) is “in tune” with the Most Harmonic Numbers when using a 12-TET instrument, the other tones will still be off their perfect pitch.
- Naturally having to change the Concert Pitch during a performance can be rather inconvenient. The concert pitches for A4 in the list ranges between 430Hz and 436Hz.
- Instruments that can not change the concert pitch – or might be too hard to intonate when using with another concert pitch then they were designed for – can be re-pitched in post production (after recording). This is generally the “best option” or sometimes the “only option” when working with instruments with tone-holes / valves / pistons (conical wood winds / brass) or those that are made out of one piece (Didgeridoo, Penny Whistle, et cetera), as well as melodic percussive instruments (like Vibraphone, Marimba, et cetera). Unfortunately there is no solution for these instruments when performing live. Using hardware for ‘real-time’ re-pitching would only be possible when using instruments that do NOT generate accoustic sound.
